UJI HETEROSKEDASTISITAS DENGAN R (BREUSCH-PAGAN TEST)

Heteroskedastisitas adalah keadaan dimana terjadinya ketidaksamaan varian dari error untuk semua pengamatan setiap variabel bebas pada model regresi. Heteroskedastisitas merupakan kebalikan dari homoskedastisitas, dimana asumsi tersebut biasanya harus terpenuhi dalam analisis regresi ataupun analisis time series. Heteroskedastisitas menyebabkan efek serius terhadap estimasi OLS (ordinary least square). Meski estimasi tetap unbiased, namun selang kepercayaan dan tes hipotesis tak dapat lagi dipercaya (unreliable)^[1].

Pada analisis regresi, heteroskedastisitas dapat didefinisikan sebagai penyebaran nilai error/residual diantara nilai estimasi. Untuk memenuhi asumsi homoskedastisitas (salah satu asumsi dalam analisis regresi linear dengan OLS), varian dari error harus selalu konstan. Untuk mengidentifikasi keberadaan heteroskedastisitas, kita dapat melakukan pengecekan dengan melihat residual plot, yaitu dengan membuat plot antara nilai residual model dengan nilai estimasi variabel Y.

Dalam model regresi sederhana (dengan 1 (satu) variabel X), kita bisa melihat apakah kondisi heteroskedastisitas terjadi. Gambar 1 menunjukkan bahwa model tersebut tidak mengalami heteroskedastisitas (homoskedastisitas). Terlihat dari sebaran nilai error yang konstan atau tetap pada semua nilai amatan. 

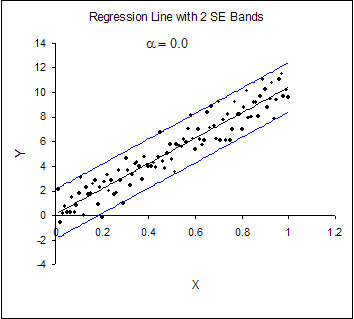Gambar 1. Contoh kondisi homoskedastisitas

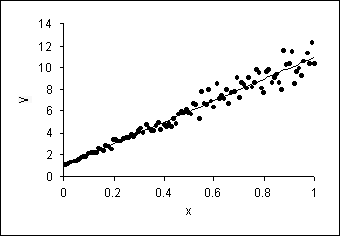
Sebaliknya, gambar 2 menunjukkan indikasi heteroskedastisitas pada model. Kondisi tersebut ditunjukkan dengan sebaran error atau varians error yang semakin membesar (semakin menyebar) seiring peningkatan nilai variabel X. Kondisi sebaliknya juga dapat terjadi, dimana sebaran error semakin membesar seiring semakin kecilnya nilai X, seperti yang terjadi pada Gambar 3. Salah satu penyebab heteroskedastisitas adalah besarnya range atau selisih antara nilai amatan.

Gambar 2. Contoh kondisi heteroskedastisitas

Gambar 3. Contoh kondisi heteroskedastisitas

Jika memiliki kecurigaan bahwa varians dari error dalam model yang kita miliki tidak homogen, maka dapat dilakukan uji statistik untuk mengidentifikasi keberadaan heteroskedastisitas. Beberapa uji statistik telah dikembangkan, dan kita akan mencoba menggunakannya dengan Aplikasi R. Uji heteroskedastisitas umumnya memiliki hipotesis sebagai berikut:

        H0    : varians dari error homoskedastik

        Ha    : varians dari error heteroskedastik

Breusch-Pagan Test

Uji ini dikembangkan oleh Breusch dan Pagan pada tahun 1979, lalu dikembangkan lagi oleh Koenker pada tahun 1981. Sehingga uji ini sering juga disebut sebagai Breusch-Pagan dan Koenker test. Pada R-Programming, kita dapat melakukan uji Breusch-Pagan dengan terlebih dahulu menginstall library olsrr.

Sebelum membentuk model dan melakukan uji heteroskedastisitas, terlebih dahulu lakukan instalasi library olsrr pada aplikasi R-Programming anda. Cara melakukan instalasi library.

>install.package(olsrr)
>library(olsrr)

Sintaks yang akan kita gunakan adalah sebagai berikut.

>model <-lm(mpg ~ disp + hp + wt + drat, data = mtcars)

>ols_test_breusch_pagan(model, rhs = TRUE)

Data yang kita gunakan merupakan data yang telah tersedia dalam R Programming, yaitu data mtcars. Jika ingin mengganti dengan data milik kita, maka kita tinggal mengganti data tersebut dengan data milik kita. Setelah kita membentuk model dan melakukan Uji Heteroskedastisitas dengan BP Test. Maka akan muncul hasil seperti berikut.

 Breusch Pagan Test for Heteroskedasticity

 -----------------------------------------

 Ho: the variance is constant            

 Ha: the variance is not constant        

           Data            

 --------------------------

 Response : mpg 

 Variables: disp hp wt drat 

        Test Summary         

 ----------------------------

 DF            =    4 

 Chi2          =    1.513808 

 Prob > Chi2   =    0.8241927 

Hasil uji menunjukkan bahwa p-value yang dihasilkan adalah sebesar 0,824. Oleh karena itu, berdasarkan hipotesis yang ada dalam uji, tak terdapat cukup bukti untuk menolak H0. Sehingga, berdasarkan uji tersebut, model yang kita miliki memenuhi asumsi homoskedastisitas (tidak ada heteroskedastisitas).

Contoh dengan data yang memiliki permasalahan heteroskedastisitas.

Contoh berikutnya adalah menggunakan data trees yang juga telah tersedia dalam R-Programming. 

>model<-lm(Volume~Height, data = trees)

>ols_test_breusch_pagan(model)

Akan menghasilkan output sebagai berikut:

 Breusch Pagan Test for Heteroskedasticity

 -----------------------------------------

 Ho: the variance is constant            

 Ha: the variance is not constant        

               Data                

 ----------------------------------

 Response : Volume 

 Variables: fitted values of Volume 

         Test Summary          

 ------------------------------

 DF            =    1 

 Chi2          =    7.490146 

 Prob > Chi2   =    0.006203754 

Berdasarkan hasil p-value yang signifikan (<0,05) dapat kita simpulkan bahwa kita menolak hipotesis nol dan menyimpulkan bahwa model tersebut memiliki permasalahan heteroskedastisitas.